📐 Giải Mã Tích Phân & Ứng Dụng: Nắm Chắc Công Thức, Xử Lý Gọn Bài Toán Diện Tích và Thể Tích

Tích Phân và Ứng Dụng là một trong những chuyên đề có tính ứng dụng cao nhất của chương trình Toán 12. Nó không chỉ kiểm tra khả năng tính toán mà còn đòi hỏi khả năng tư duy hình học. Thầy Phạm Tín sẽ hướng dẫn các em nắm chắc nền tảng và phương pháp giải quyết các bài toán liên quan đến diện tích hình phẳng và thể tích vật thể.

I. Tích Phân: Nền Tảng Của Mọi Bài Toán Ứng Dụng

Nắm vững định nghĩa và các tính chất cơ bản của Tích phân là điều kiện tiên quyết.

1. Định Nghĩa và Tính Chất Cơ Bản

Tích phân xác định của hàm số f(x) liên tục trên đoạn [a,b] được định nghĩa là:

∫ab​f(x)dx=F(b)−F(a)

Trong đó, F(x) là một nguyên hàm của f(x).

Các tính chất quan trọng cần nhớ:

• ∫ab​[f(x)±g(x)]dx=∫ab​f(x)dx±∫ab​g(x)dx
• ∫ab​k⋅f(x)dx=k⋅∫ab​f(x)dx
• ∫ab​f(x)dx=∫ac​f(x)dx+∫cb​f(x)dx(a<c<b)

2. Hai Phương Pháp Tính Tích Phân Cốt Lõi

1. Phương pháp Đổi Biến Số: Chọn t=g(x). Điều chỉnh vi phân (dt=g′(x)dx) và Đổi Cận (x=a→t=g(a), x=b→t=g(b)).
2. Phương pháp Tích Phân Từng Phần: Áp dụng công thức:
3. ∫ab​udv=[uv]ab​−∫ab​vdu
4. Thầy Tín khuyến nghị: Hãy ưu tiên chọn u theo thứ tự: Logarit, Đa thức, Mũ, Lượng giác.

II. Ứng Dụng 1: Tính Diện Tích Hình Phẳng

Bài toán diện tích hình phẳng luôn yêu cầu học sinh phải xác định chính xác cận tích phân và hàm số nào nằm trên/nằm dưới.

1. Diện tích giới hạn bởi một hàm số và trục hoành

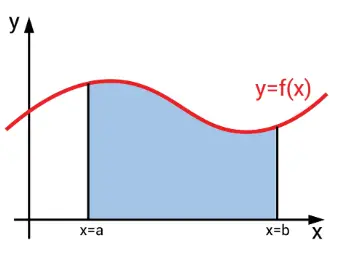
Diện tích S của hình phẳng giới hạn bởi đồ thị y=f(x), trục hoành y=0, và hai đường thẳng x=a,x=b:

S=∫ab​∣f(x)∣dx

💡 Lời khuyên của Thầy Tín: Nếu f(x) đổi dấu trên [a,b], hãy chia tích phân thành nhiều đoạn để khử dấu giá trị tuyệt đối, hoặc sử dụng máy tính Casio để kiểm tra nhanh.

Tích Phân và Ứng Dụng là một trong những chuyên đề có tính ứng dụng cao nhất của chương trình Toán 12. Nó không chỉ kiểm tra khả năng tính toán mà còn đòi hỏi khả năng tư duy hình học. Thầy Phạm Tín sẽ hướng dẫn các em nắm chắc nền tảng và phương pháp giải quyết các bài toán liên quan đến diện tích hình phẳng và thể tích vật thể.

I. Tích Phân: Nền Tảng Của Mọi Bài Toán Ứng Dụng

Nắm vững định nghĩa và các tính chất cơ bản của Tích phân là điều kiện tiên quyết.

1. Định Nghĩa và Tính Chất Cơ Bản

Tích phân xác định của hàm số $f(x)$ liên tục trên đoạn $[a, b]$ được định nghĩa là:

$$\int_{a}^{b} f(x) dx = F(b) - F(a)$$

Trong đó, $F(x)$ là một nguyên hàm của $f(x)$.

Các tính chất quan trọng cần nhớ:

• $$\int_{a}^{b} [f(x) \pm g(x)] dx = \int_{a}^{b} f(x) dx \pm \int_{a}^{b} g(x) dx$$
• $$\int_{a}^{b} k \cdot f(x) dx = k \cdot \int_{a}^{b} f(x) dx$$
• $$\int_{a}^{b} f(x) dx = \int_{a}^{c} f(x) dx + \int_{c}^{b} f(x) dx \quad (a < c < b)$$

2. Hai Phương Pháp Tính Tích Phân Cốt Lõi

1. Phương pháp Đổi Biến Số: Chọn $t = g(x)$. Điều chỉnh vi phân ($dt = g'(x) dx$) và Đổi Cận ($x=a \rightarrow t=g(a)$, $x=b \rightarrow t=g(b)$).
2. Phương pháp Tích Phân Từng Phần: Áp dụng công thức:
3. $$\int_{a}^{b} u dv = [uv]_{a}^{b} - \int_{a}^{b} v du$$
4. Thầy Tín khuyến nghị: Hãy ưu tiên chọn $u$ theo thứ tự: Logarit, Đa thức, Mũ, Lượng giác.

II. Ứng Dụng 1: Tính Diện Tích Hình Phẳng

Bài toán diện tích hình phẳng luôn yêu cầu học sinh phải xác định chính xác cận tích phân và hàm số nào nằm trên/nằm dưới.

1. Diện tích giới hạn bởi một hàm số và trục hoành

Diện tích $S$ của hình phẳng giới hạn bởi đồ thị $y = f(x)$, trục hoành $y=0$, và hai đường thẳng $x=a, x=b$:

$$S = \int_{a}^{b} |f(x)| dx$$💡 Lời khuyên của Thầy Tín: Nếu $f(x)$ đổi dấu trên $[a, b]$, hãy chia tích phân thành nhiều đoạn để khử dấu giá trị tuyệt đối, hoặc sử dụng máy tính Casio để kiểm tra nhanh

2. Diện tích giới hạn bởi hai hàm số

Diện tích $S$ của hình phẳng giới hạn bởi hai đồ thị $y = f(x)$, $y = g(x)$ và hai đường thẳng $x=a, x=b$:

$$S = \int_{a}^{b} |f(x) - g(x)| dx$$

• Trường hợp đặc biệt: Nếu đề bài không cho $a, b$, ta phải giải phương trình hoành độ giao điểm $f(x) = g(x)$ để tìm ra các cận $a, b$.

III. Ứng Dụng 2: Tính Thể Tích Vật Thể Tròn Xoay

Bài toán thể tích thường liên quan đến hình phẳng quay quanh trục hoành hoặc trục tung.

1. Thể tích vật thể tròn xoay quanh trục $Ox$

Thể tích $V$ của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi $y = f(x)$, trục $Ox$ và $x=a, x=b$ quanh trục $Ox$:

$$V = \pi \int_{a}^{b} [f(x)]^2 dx$$

2. Thể tích vật thể tròn xoay quanh trục $Oy$

Thể tích $V$ của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi $x = g(y)$, trục $Oy$ và $y=c, y=d$ quanh trục $Oy$:

$$V = \pi \int_{c}^{d} [g(y)]^2 dy$$

⚠️ Thầy Tín Cảnh Báo: Khi quay quanh trục $Oy$, phải biến đổi hàm số về dạng $x = g(y)$ và tính theo cận $y$.

IV. Luyện Tập Đỉnh Cao Cùng Thầy Phạm Tín

Tích phân là chuyên đề rất dễ ghi điểm nếu các em làm đúng phương pháp và cẩn thận trong tính toán. Tại Trung tâm THÀNH CÔNG, các em sẽ được:

1. Luyện tập chuyên sâu: Hàng trăm bài tập Tích phân từ cơ bản đến nâng cao, đảm bảo không bỏ sót dạng toán nào.
2. Kỹ thuật giải nhanh: Hướng dẫn sử dụng công thức tính nhanh cho một số hình phẳng đặc biệt (ví dụ: Parabol và đường thẳng).
3. Tối ưu Casio: Sử dụng máy tính để kiểm tra kết quả Tích phân và Diện tích một cách hiệu quả, hạn chế sai sót.

Hãy đăng ký khóa học Toán 12 ngay hôm nay để làm chủ Tích Phân và các bài toán Ứng Dụng!

Khám phá

2. Diện tích giới hạn bởi hai hàm số

Diện tích S của hình phẳng giới hạn bởi hai đồ thị y=f(x), y=g(x) và hai đường thẳng x=a,x=b:

S=∫ab​∣f(x)−g(x)∣dx

• Trường hợp đặc biệt: Nếu đề bài không cho a,b, ta phải giải phương trình hoành độ giao điểm f(x)=g(x) để tìm ra các cận a,b.

III. Ứng Dụng 2: Tính Thể Tích Vật Thể Tròn Xoay

Bài toán thể tích thường liên quan đến hình phẳng quay quanh trục hoành hoặc trục tung.

1. Thể tích vật thể tròn xoay quanh trục Ox

Thể tích V của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi y=f(x), trục Ox và x=a,x=b quanh trục Ox:

V=π∫ab​[f(x)]2dx

2. Thể tích vật thể tròn xoay quanh trục Oy

Thể tích V của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi x=g(y), trục Oy và y=c,y=d quanh trục Oy:

V=π∫cd​[g(y)]2dy

IV. Luyện Tập Đỉnh Cao Cùng Thầy Phạm Tín

Tích phân là chuyên đề rất dễ ghi điểm nếu các em làm đúng phương pháp và cẩn thận trong tính toán. Tại Trung tâm THÀNH CÔNG, các em sẽ được:

1. Luyện tập chuyên sâu: Hàng trăm bài tập Tích phân từ cơ bản đến nâng cao, đảm bảo không bỏ sót dạng toán nào.
2. Kỹ thuật giải nhanh: Hướng dẫn sử dụng công thức tính nhanh cho một số hình phẳng đặc biệt (ví dụ: Parabol và đường thẳng).
3. Tối ưu Casio: Sử dụng máy tính để kiểm tra kết quả Tích phân và Diện tích một cách hiệu quả, hạn chế sai sót.

Hãy đăng ký khóa học Toán 12 ngay hôm nay để làm chủ Tích Phân và các bài toán Ứng Dụng!